Claudio Ptolomeo

—La summa de la astronomía antigua y de las ciencias afines.—

A pesar de la enorme importancia de Claudio Ptolomeo en la historia de la ciencia en el ámbito griego tardoantiguo, en el islam medieval y en la Europa de la Baja Edad Media y renacentista, los datos biográficos que tenemos sobre él son muy escasos. Todo lo que sabemos, extraído de su obra, es que realizó observaciones astronómicas en Alejandría entre el 125 y el 141 d. C. (que utilizó en su gran obra, el Almagesto). También dedicó una inscripción astronómica en un santuario de Serapis en Canopo, no muy lejos de Alejandría, de la que solo conservamos copias del texto en los manuscritos medievales. Podemos deducir, pues, que su lugar de residencia principal era Alejandría, en el Egipto grecorromano del segundo siglo de nuestra era.

Claudius Ptolemaeus Alexandrinus, de Pedro Berruguete o Joos van Gent (Musée du Louvre). Wikimedia.

El nombre “Ptolomeo” era muy popular en la provincia de Egipto, por haber sido el nombre de los gobernantes masculinos de la dinastía macedónica que se instaló allí en la época helenística. Sin duda, este nombre y la falta de otras informaciones biográficas promovieron la suposición errónea de que Claudio Ptolomeo fue un rey egipcio, la cual vemos reflejada en la corona y la ropa regia del retrato que originalmente decoraba el studiolo de Federico da Montefeltro en el palacio ducal de Urbino; dentro del grupo de 28 retratos de personalidades antiguas y modernas relacionadas con el mundo del conocimiento, Ptolomeo figuraba al lado de los filósofos Platón, Aristóteles y Boecio.

El equívoco con los monarcas helenísticos ya lo encontramos en fuentes árabes anteriores como Abu Ma‘shar (s. IX), que en su Gran introducción a los juicios de las estrellas (IV 1) dice que Ptolomeo “el sabio”, quien compuso el Almagesto, fue uno de los reyes Ptolomeos que gobernaron Egipto después de Alejandro Magno. Curiosamente, a renglón seguido, Abu Ma‘shar pone en duda que fuera el mismo autor que escribió la obra astrológica llamada Tetrabiblos; duda que resurgió entre los estudiosos alemanes del siglo XIX, que no creían que un autor de una astronomía matemática compleja como la del Almagesto hubiera escrito un libro de astrología. Volviendo al retrato del studiolo de Urbino, que puede ser de Pedro Berruguete o de Joos van Gent, el turbante sería una mera indicación de que nuestro sabio era del norte de África, pero el instrumento que lleva en la mano sí tiene una tradición auténtica, ya que Ptolomeo mismo describe su construcción en el Almagesto (V 1): se trata de un astrolabio esférico o esfera armilar, que servía tanto para visualizar la compleja geometría esférica de los movimientos celestes (la tierra estaba representada como la bola central) como para hacer de manera sencilla y aproximada cálculos astronómicos complejos que requerían el uso de tablas.

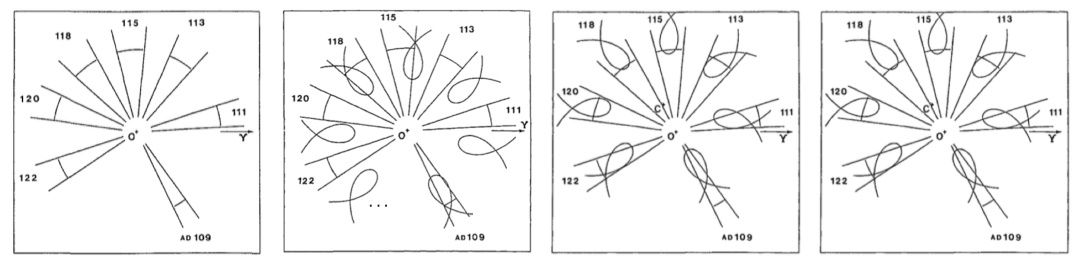
Arcos de retrogradación de Marte entre los años 109 y 122 d. C. (1), superpuestos a los tirabuzones descritos por un epiciclo (2), por un epiciclo con órbita excéntrica (3) y por un epiciclo con órbita excéntrica y ecuante (4). Evans, James. The history and practices of ancient astronomy. Oxford: OUP; 1998.

Claudio Ptolomeo es, por decirlo de alguna manera, el astrónomo antiguo: su teoría planetaria conseguía finalmente modelar geométricamente y de manera precisa los movimientos de los cuerpos astrales. Esto era gracias a la invención del ecuante —probablemente atribuible a él mismo, aunque el autor prefiere mantener un perfil bajo (pero a la vez universalizante) aquí como en casi todas sus obras—; el ecuante representaba un tercer elemento concebido como centro desplazado de velocidad angular uniforme que, sumado al epiciclo y a la órbita excéntrica, contribuía a describir la longitud a lo largo de la eclíptica (la eclíptica es el camino del sol a lo largo del año desde la perspectiva geocéntrica) de las órbitas planetarias en toda su irregularidad.

Hiparco (s. II a. C.) ya había construido una teoría geométrica para los movimientos del sol y de la luna —de la que solo podemos leer referencias dentro del Almagesto y de los comentarios antiguos al Almagesto, de Teón y Papo—, pero no para los planetas. Los astrónomos y astrólogos griegos conocieron los métodos iterativos aritméticos usados desde el siglo V a. C. por los babilonios (tenemos testimoniado su uso en papiros griegos de época imperial romana), pero Hiparco y Ptolomeo iban por otro camino, a pesar de que se sirvieron de la tradición astronómica babilónica para sus observaciones y para algunos parámetros.

Ptolomeo pudo usar desarrollos de la geometría esférica griega como el teorema de Menelao (siglo I d. C.), lo cual no hubiera sido posible en la época clásica, en la que la geometría de sólidos se encontraba en un estado poco desarrollado, tal y como se lamenta Platón en el libro VII de la República. En todo caso, Ptolomeo debió de vivir su gesta a la manera del heurēka arquimediano, ya que grabó su teoría astronómica en forma de una lista de parámetros en la citada inscripción de Canopo en agradecimiento al dios. Por cierto, tenemos otro ejemplo de esta práctica tan curiosa, la inscripción astronómica hallada en Keskinto, Rodas, que fue dedicada a “todos los dioses y diosas” por un astrónomo anónimo probablemente en el siglo I a. C.

Ptolomeo escribió la obra total de la astronomía antigua, el Almagesto. Este carácter ya se refleja en su título original (Composición astronómica), pero aún más en la arabización del griego megistē, ‘la más grande (sc. composición)’, que ha acabado dando su nombre más popular. Por eso la obra de Ptolomeo se copió y se conservó, pero no la de Hiparco, de un carácter más parcial. Pero es que, además del Almagesto, Ptolomeo escribió unas cuantas obras astronómicas más, todas dedicadas a un desconocido Siro, cuyo nombre significa ‘sirio’, lo cual probablemente indica un origen en esa región y un linaje servil. No sabemos si era un patrón rico o un joven interesado en la astronomía, pero probablemente Ptolomeo no lo veía como a un colega a su nivel, ya que de lo contrario nos podríamos esperar que lo hubiera hecho constar. En todo caso, él y un tal Teón, de quien toma una serie de observaciones astronómicas (Almagesto IX 9, X 1-2) son los únicos contemporáneos que menciona en toda su obra. La sensación general es de soledad: a diferencia del mundo islámico medieval, donde tenemos testimoniados numerosos contactos y colaboraciones entre matemáticos, el mundo astronómico griego es más bien pequeño, incluso si contamos con el factor de la menor conservación de las fuentes.

Primera página del calendario de Fases de las estrellas fijas en la edición de Heiberg: “Toth (~septiembre) 1r (día): 14 ½ horas (=latitud correspondiente a 14 ½ horas solares en el solsticio=latitud de Rodas): la estrella de la cola de Leo sale (=sale al mismo tiempo que el sol por el horizonte); según Hiparco, los vientos estivales se detienen; según Eudoxo, lluvia, tormentas, y los vientos estivales se detienen./ 2o (día): 14 horas (=latitud correspondiente a 14 horas solares en el solsticio=latitud del Bajo Egipto): la estrella de la cola de Leo sale, y Spica se pone; según Hiparco, cambio de tiempo. 3r (dia) (…)”. Heiberg, J. L., Claudii Ptolemaei Opera astronomica minora. Lepzig: Teubner; 1907.

Del resto de obras astronómicas, un par son derivadas del Almagesto: las Hipótesis planetarias, donde describe un modelo físico que podría servir de base para un planetario, incorporando la teoría astronómica del Almagesto, y las Tablas manejables, formada por un conjunto de tablas astronómicas derivadas de las de esta misma obra, y formateadas de manera conveniente para los astrólogos (pero no de manera declarada). Las otras tres tratan cuestiones de proyección de la esfera en el plano —el Analemma en relación al movimiento solar observado en las sombras sobre la Tierra y el Planisferio para el mapa de las estrellas fijas— y las salidas y puestas de las estrellas fijas (Fases de las estrellas fijas).

Sin llegar a cubrir tantos campos del saber como un al-Kindi o un Avicena, Ptolomeo ya adopta en cierto modo la figura que siglos más tarde veremos en los sabios islámicos. En efecto, además de astronomía (sin duda su campo predilecto), Ptolomeo cultivó la astrología, la geografía, la teoría musical y la epistemología. Su texto astrológico —Tetrabiblos, ‘Cuatro libros’, originalmente intitulado Apotelesmatika, ‘Efectos astrológicos’— no es ni mucho menos una obra desdeñable, sino que representa un esfuerzo enorme de síntesis y a la vez de explicación lo más racional posible de las doctrinas astrológicas más corrientes de la época, precedida por una introducción donde desarrolla una defensa de la posibilidad y la utilidad del arte astrológico.

La astrología grosso modo como la conocemos hoy en día había sido creada en el mundo grecorromano del siglo II a. C. (concretamente en Egipto) a partir de elementos mayoritariamente babilónicos, y en la época de Ptolomeo disfrutaba de un cierto éxito en todas las capas de la sociedad; pero también era puesta en duda, como testimonia Cicerón en Sobre la adivinación. A diferencia de la práctica de adivinación astral en el mundo babilónico, desarrollada internamente y por parte de escribas asociados a los templos principales, en el mundo grecorromano la astrología había sido implantada al lado de disciplinas que se entendían hasta cierto punto como racionales y autojustificadas, como la medicina o la matemática. Por eso los primeros tratados astrológicos griegos eran en forma poética y supuestamente inspirados por la divinidad; poco a poco fueron surgiendo tratados en prosa, el más científico de los cuales fue el de Ptolomeo.

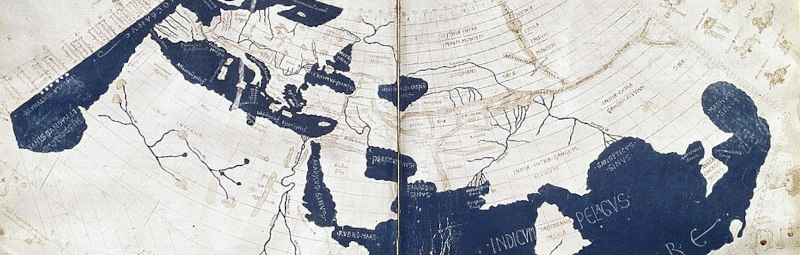
Mapa conservado en el original griego de la oikoumenē gē (‘tierra habitada’) en la primera proyección propuesta en la Guía de geografía, ilustrado por Francesco di Antonio del Chierico a partir de la traducción latina de Jacopo d’Angelo. Harleian MS 7182, ff. 58-59 (ca. 1465-1470). Wikimedia.

El tratado de geografía (Guía de geografía) de Ptolomeo ya se apunta como proyecto futuro en el Almagesto (II 13). Se trata de una obra voluminosa, en ocho libros, seis de los cuales consisten en una larga tabla (o más bien una lista) con las coordenadas de las principales ciudades y accidentes geográficos (unos 8.000 puntos) dentro del rectángulo de tierra conocida en el mundo grecorromano del momento (la oikoumenē gē, ‘tierra habitada’), computadas en longitud este desde las Islas de los Bienaventurados (identificadas con las Canarias), y en latitud norte y sur partiendo del ecuador.

Las medidas geográficas se obtenían tanto de observaciones astronómicas como de estimaciones basadas en informaciones de viajeros. Las medidas en longitud eran el mayor problema, y no resulta sorprendente que justamente el mayor error de la obra sea una sobreestimación general en esta coordenada. La Guía de geografía representa el segundo atlas geográfico-matemático del que tenemos constancia: se piensa que originalmente contenía mapas, que desaparecieron y se reconstruyeron en el Renacimiento. Como de costumbre, conocemos la tradición anterior gracias a la misma obra de Ptolomeo, ya que comienza con una crítica al atlas de Marino de Tiro (entre los siglos I y II d. C.) por adecuarse solo a una geografía limitada en el espacio y por representar meridianos y paralelos con líneas rectas paralelas. Ptolomeo propone proyecciones más adecuadas de la esfera sobre el plano.

El instrumento de Oriente Medio llamado qānūn recibe su denominación del instrumento del teórico musical griego antiguo (kanōn). Wikimedia.

Otra obra de Ptolomeo es la Armónica (literalmente, ‘Cosas en relación con la armonía’), la cual es de gran interés para la historia de la música y de teoría musical. Este texto toma el relevo de proyectos anteriores —desde el antiguo pitagórico Arquitas (siglos V-IV a. C.) hasta el más cercano en el tiempo Dídimo (siglo I d. C.)— que describían matemáticamente, en términos de proporciones numéricas, las escalas musicales usadas en la práctica musical. Igual que Dídimo, Ptolomeo utiliza un instrumento propio de los teóricos de la música griega, inventado en época helenística, el kanōn, consistente en una o múltiples cuerdas tensadas sobre una superficie plana y reglada, con unos puentes móviles que permitían medir la longitud de las cuerdas. El instrumento de Oriente Medio llamado qānūn es deudor de esta denominación griega, si bien probablemente tienen tradiciones independientes. El kanōn se utiliza para comprobar con la audición las distancias interválicas propuestas por el teórico musical: Ptolomeo mismo explica su construcción, de manera que el lector en principio podía hacer todas las comprobaciones que se indican en el tratado. El punto culminante del texto son una serie de tablas que describen con toda precisión la posición de los puentes que reproducían todas las notas de las escalas tradicionales griegas, en todos los modos posibles. El tratado también es interesantísimo por su discusión epistemológica, que incorpora definiciones musicales del peripatético Aristoxeno, y también por la sección final, consistente en un excurso que pone en relación los elementos pitagórico-platónicos de la música con la teoría desarrollada en el mismo tratado.

Finalmente, cabe destacar el breve ensayo llamado Sobre el criterio y la parte regente, de contenido únicamente epistemológico, sin ninguna referencia concreta a temas matemáticos, pero de clara aplicación como fundamento teórico de sus otros tratados. De hecho, en el texto de la Armónica aparecen en una forma más sucinta algunos de los temas de este ensayo. Ptolomeo presenta en él el concepto originalmente estoico de ‘criterio’ (kritērion), que posteriormente (ya en su época) fue compartido por otras escuelas filosóficas y por científicos interesados en desarrollar una teoría del conocimiento, como el médico Galeno.

En origen, se trataba, para los estoicos, de proponer la existencia de una herramienta epistemológica para establecer la verdad de una hipótesis frente al resto, para llegar a un conocimiento válido. Hemos de situar esta discusión en el contexto de la pugna entre estoicos y académicos (platónicos) por la cuestión de la posibilidad del conocimiento, en la que los últimos proponían la epokhē o abstención de juicio, la cual hacía impracticable, o al menos difícil, la noción de ciencia. La aplicación del criterio a ciencias como la astronomía es propuesta por primera vez explícitamente por el estoico Posidonio (principios del siglo I a. C.), y de algún modo implica una continuidad entre la filosofía natural, tradicionalmente practicada desde una cierta distancia por parte del filósofo, y las ciencias matemáticas. El mismo Posidonio es filósofo y a la vez matemático.

Que Ptolomeo es heredero de esta tradición, y que tiene un interés evidente en presentarse como un filósofo (además de astrónomo y matemático), se hace evidente ya en el inteligente e intricado prefacio del Almagesto, en el que define y clasifica la astronomía y la matemática como disciplinas internas a la filosofía, utilizando declaradamente (pero de una manera levemente sesgada) una antigua clasificación de la Metafísica de Aristóteles (1026a). La referencia al antiguo maestro tampoco es casual, ya que de alguna manera el proyecto ptolemaico de tratar todos los campos de la matemática aplicada tiene un paralelo con el enciclopedismo peripatético. En efecto, nadie antes que Ptolomeo había estudiado en profundidad y de manera interconectada disciplinas de la matemática aplicada como la astronomía, la astrología, la geografía y la teoría musical.

Cristian Tolsa
Universitat de Barcelona

* Traducción: Judit Gil-Farrero

Cómo citar este artículo:
Tolsa, Cristian. Claudio Ptolomeo. Sabers en acció, 2025-02-05. https://sabersenaccio.iec.cat/es/claudio-ptolomeo/.

Para saber más

Puedes ampliar la información con la bibliografía y recursos disponibles.