Las ciencias en Bagdad

—La astronomía, la astrología y las disciplines matemáticas durante el siglo IX.—

La disciplina más importante durante el califato de al-Manṣūr fue la astrología, que era considerada como una ciencia de acuerdo con la epistemología aristotélica. Al-Kindī (m. 876), el gran filósofo de la época, y su discípulo Abū Maʿxar (787-886), uno de los astrólogos más importantes, lo sostuvieron con firmeza y buenos argumentos. Los astrólogos de al-Manṣūr eran mayoritariamente de origen persa (Nawbakht y su numerosa descendencia, Māixāʾallāh, ʿUmar ibn Farrukhān al-Ṭabarī), aunque había otros de origen árabe como al-Fazārī o Yaʿqūb ibn Ṭāriq. La astrología que practicaban debía de ser esencialmente la persa, que empleaba los textos de autores griegos como Doroteo de Sidón traducidos al pehlevi, algunos de los cuales fueron traducidos al árabe por estos astrólogos. Estos autores eran (también y sobre todo si querían ser buenos astrólogos) unos astrónomos más que competentes que se proveyeron de los mejores medios posibles, empezando por tablas astronómicas. Algunas ya las tenían en su bagaje persa (Zīj al-Arkand y Zij al-Xāh), y el año 771 o 773 llegó a Bagdad una embajada de la India en la que había un astrónomo que llevaba el Brahmasphutasidhānta, las tablas astronómicas compiladas por el hindú Brahmagupta en 629. Con la ayuda de aquel astrónomo, al-Fazārī y Yaʿqūb ibn Ṭāriq tradujeron estas tablas que en lo sucesivo serían conocidas como Sindhind y llegarían hasta al-Andalus. No se quedaron ahí y al-Fazārī pasa por ser el primer constructor musulmán de un astrolabio, inaugurando así una fértil tradición que tenía pocos precedentes en el mundo griego y siríaco y que posiblemente los autores de Bagdad conocieron a través de fuentes siríacas. Por su parte, Māixāʾallāh escribió un tratado cosmológico en el que citaba a Ptolomeo y Aristóteles, probablemente conocidos también a través de traducciones siríacas.

Página del tratado astrológico sobre natividades de Abū Maʿxar. Se encuentra en un manuscrito egipcio del s. XV (BNF Arabe 2583). Wikimedia.

Al-Maʾmūn dio un fuerte impulso a la astronomía rodeándose de una nueva generación de astrónomos/astrólogos entre los que había personas muy brillantes como al-Kwārizmī, Ḥabaix al-Ḥāsib, los hermanos Banū Mūsā o Yaḥyā b. Abī Manṣūr o el menos conocido, en términos bbiográficos, al-Farghānī. Obsesionado por la precisión, al-Maʾmūn ordenó que se hicieran observaciones del cielo para verificar los parámetros de Ptolomeo (para entonces ya se habían hecho dos traducciones del Almagesto, se tradujo una tercera vez para al-Maʾmūn y aún se harían otras dos versiones más en el siglo IX). Las primeras observaciones se hicieron entre 828 y 829 en un barrio de Bagdad llamado Xammasiyya y como no quedaron del todo satisfechos con ellas, hicieron otras nuevas en Damasco entre 831 y 832.

En estos lugares se construyeron sendos observatorios, los primeros en la historia del islam, que probablemente se equiparon con instrumentos de observación similares a los descritos por Ptolomeo en el Almagesto. De las observaciones hechas se derivaron diversas tablas astronómicas comenzando por la oficial, que se llamó al-Zīj al-mumtaḥan, “las tablas comprobadas”, compiladas por Yaḥyā b. Abī Manṣūr. Entre los parámetros que se corrigieron a Ptolomeo para ajustarlos más a la realidad hay algunos tan importantes como la oblicuidad de la eclíptica (23;51° según Ptolomeo, 23;33° según Yaḥyā b. Abī Manṣūr) o la precesión de los equinoccios (1° por siglo según Ptolomeo, 1° en 66 años siguiendo modelos indopersas). Algunos de estos astrónomos como al-Khwārizmī o Ḥabaix hicieron sus propias tablas, el primero revisando las del Sindhind y el segundo revisando las tablas indopersas en su juventud y las Mumtaḥan al final de su vida.

Estos astrónomos sobresalieron igualmente en el terreno de la instrumentación. Al-Khwārizmī es el autor del primer tratado de construcción y uso del astrolabio y a Ḥabaix se le atribuye la invención del astrolabio esférico y, además, escribió un tratado sobre un astrolabio curioso con forma de melón. Estos astrónomos también se preocuparon por los modelos cosmológicos y ya Muḥammad ibn Mūsā escribió diversos tratados cuestionando los modelos planetarios de Ptolomeo, y, específicamente, criticando que este postulara la existencia de una novena esfera para explicar el movimiento diurno de los astros. Esta línea de trabajo continuó hasta finales de siglo y prosperó notablemente en el futuro, dando lugar a una fértil tradición de estudios y modelos de cosmología matemática que llegaría a conocer el mismo Copérnico. Si bien mucha de la astronomía que se practicó tenía como finalidad la confección de los horóscopos más perfectos posibles, hay que tener en cuenta que había un interés sincero por hacer buena ciencia y para que esta ciencia fuera útil. En este sentido, los astrónomos de esta época se esforzaron para poner la astronomía al servicio del culto islámico. Tres aspectos fueron de especial importancia: la determinación de la aparición del creciente lunar, porque marcaba el inicio del mes en el calendario islámico y había que saber cuándo comenzaba el mes del Ramadán si las nubes ocultaban la luna; la determinación de las horas de plegaria, especialmente las de mediodía y primera de la tarde porque dependen de la sombra proyectada por un gnomon; y la determinación de la dirección de la Meca (quibla, alquibla) para poder orientar bien las mezquitas, para lo cual los astrónomos crearon procedimientos geométricos y trigonométricos de gran exactitud.

Junto con esta ciencia tan sofisticada, los filólogos y literatos compilaron, con la intención de preservar el léxico y la paremiología popular de los árabes, sus conocimientos que podemos relacionar con la ciencia. En este caso, se trata de la astronomía popular árabe, relacionada con el uso de las estrellas que hacían los beduinos para orientarse, y a su conocimiento empírico de las estrellas, el sol y la luna, como marcadores temporales, que, además, estaban vinculados a la aparición de fenómenos meteorológicos recurrentes. Las tan escasas como deseadas lluvias eran el elemento esencial de este conocimiento que hoy podemos llamar etnociencia y que entonces se compiló particularmente en tratados sobre anwāʾ (periodos marcados por asterismos asociados a lluvias y otros meteoros). Curiosamente, quizá una buena parte de este saber empírico nacía de una creencia astrolátrica (del estilo “las estrellas que aparecen regularmente en otoño causan las lluvias de otoño”) que el islam abolió. Pese a este problema, la etnoastronomía quedó vinculada a la nueva tradición cultural de los musulmanes porque los hombres de religión enmendaron cualquier problema legal con gran finura jurídica y la gente común apreció el valor del legado tradicional y su utilidad para, por ejemplo, determinar de forma muy aproximada la alquibla. A pesar de su carácter no científico, es curioso constatar cómo los autores de estos tratados se apropiaron de conceptos de la astronomía indopersa de los astrónomos científicos (según los estándares de la época).

Pero este tipo de conocimiento es periférico en el saber de la época, en el que la precisión de la ciencia impera. En el Libro de los cuerpos y las distancias de Ḥabaix al-Ḥāsib, se dice que el califa al-Maʾmūn quería saber la quibla de la Meca desde Bagdad y ordenó que se calculara la diferencia de longitudes entre la Meca y Bagdad mediante la observación de un eclipse lunar en ambas ciudades. El método ya lo habían usado Hiparco y Ptolomeo. El eclipse tiene lugar en el mismo momento pero en una hora diferente en cada ciudad. Si sabemos la diferencia de la hora entre las dos ciudades, considerando que una hora equivale a 15^o de la esfera, podemos encontrar aproximadamente la diferencia de longitud, que en el texto se estima en unos 3^o. La diferencia de latitud era fácil de calcular con solo la posición del sol. Los datos obtenidos permiten, mediante procedimientos geométricos y trigonométricos, no solo obtener la dirección de la Meca sino la distancia entre Bagdad y la Meca teniendo en cuenta cuántas millas corresponden a un grado de la esfera. En el texto, un grado corresponde a 56 millas, y la línea más directa entre las dos ciudades (la que trazaría “una flecha que volara por el aire”), se estima en 676 millas y 2/3, mientras que se constata que la distancia real del camino es de 712. El califa da por buena la diferencia dado que en el camino hay muchas subidas y bajadas. Esta reveladora anécdota se incluye en un libro que trata, esencialmente, de otra de las obsesiones de al-Maʾmūn, la determinación de la distancia exacta de la tierra para poner al día la famosa medición de Eratóstenes. Ḥabaix nos habla de una expedición ordenada por el califa a tal efecto, con un equipo de astrónomos bien provisto, y otras fuentes nos hablan de otra en la que el equipo científico estaría formado por los hermanos Banū Mūsā y, quizá, al-Khwārizmī. El problema de los relatos es que no terminan de coincidir en la equivalencia entre grados y millas árabes, pero en la aproximación más optimista (un grado, 56 millas 2/3 y una milla árabe, ca. 111,12 km), el valor de la circunferencia de la Tierra se acerca mucho al real de 40.007,863 km.

Página de un manuscrito del Libro de la forma de la tierra de al-Khwārizmī, en la que se representa el Nilo. Manuscrito Strasbourg, Bibliothèque Nationale et Universitaire, Ms 4.247. Wikimedia.

Con independencia de las discrepancias de las narrativas, parece evidente que tal expedición existió y que forma parte de otro de los proyectos de al-Maʾmūn: conocer la tierra tan bien como el cielo, lo cual tiene todo el sentido si pensamos que un gobernante debe tener el conocimiento más preciso posible del territorio. El califa dio un impulso decisivo a la geometría matemática y la cartografía, aunque los detalles del proceso aún se nos escapan. Parece ser que la Geografía de Ptolomeo (y quizá también la de Marino de Tiro) ya circulaba por Bagdad en la época de al-Maʾmūn y este habría ordenado a un equipo de geógrafos, que podía muy bien coincidir con el de astrónomos (de hecho, los principios de proyección de la cartografía son similares a los de la proyección de los instrumentos astronómicos), la preparación de unos mapas de la Tierra. Según uno de los grandes expertos en el tema, Fuat Sezgin, aún quedaría un mapamundi de estos transmitido por el geógrafo e historiador al-ʿUmarī (m. 1349). Según Sezgin, y esto es controvertido pero interesante, este mapa sería una novedad ya que Ptolomeo explica cómo hacer mapas, pero no hizo ninguno en la práctica. Lo que nos queda es un Kitāb Ṣūrat al-arḍ (Libro sobre la forma de la Tierra) de al-Khwārizmī (según Sezgin, no se tendría por qué identificarlo necesariamente con el famoso astrónomo y matemático), que consiste principalmente en una larga lista de coordenadas geográficas de muchas localidades. Este tratado es coherente con el mapa, que dibuja un mundo más realista, con un océano Índico que no es un gran lago cerrado, a diferencia de las representaciones griegas, y un mar Mediterráneo ajustado a sus verdaderas proporciones.

Otras disciplinas basadas en la matematización del mundo (como la música o la óptica) florecieron en el periodo gracias a las traducciones de las fuentes griegas. De estas, la más importante en el periodo es la estática, la ciencia “de los pesos”, que subyace tras la técnica de construcción de las balanzas y es también el principio de la mecánica desarrollada entre los griegos por Herón de Alejandría o Filón de Bizancio. Los más destacados fueron los Banū Mūsa, autores de un Kitāb al-Ḥiyal que el gran experto en el tema, Donald Hill, traduce como “Book of ingenious devices” o “Libro de los dispositivos ingeniosos”. En él se describen más de un centenar de aparatos destinados esencialmente a la diversión y a la pedagogía. Se trata de autómatas como un flautista que toca la flauta que produce música gracias a un complejo instrumento hidráulico; o de artefactos que producen toda una serie de efectos sorprendentes, como una jarra donde se vierten líquidos de tres colores diferentes y cuando se abre un grifo los líquidos salen en el orden en el que se habían metido. Se trata de un aprovechamiento lúdico de la energía del agua y el aire mediante válvulas, engranajes y pistones que, en lo sucesivo, aún se sofisticará más y permitirá disponer de ingenios más complejos para un uso civil. En cualquier caso, los Banū Mūsa y otros como al-Farghānī actuaron como ingenieros para los califas en infraestructuras complejas, aunque de las técnicas empleadas no han quedado referencias escritas.

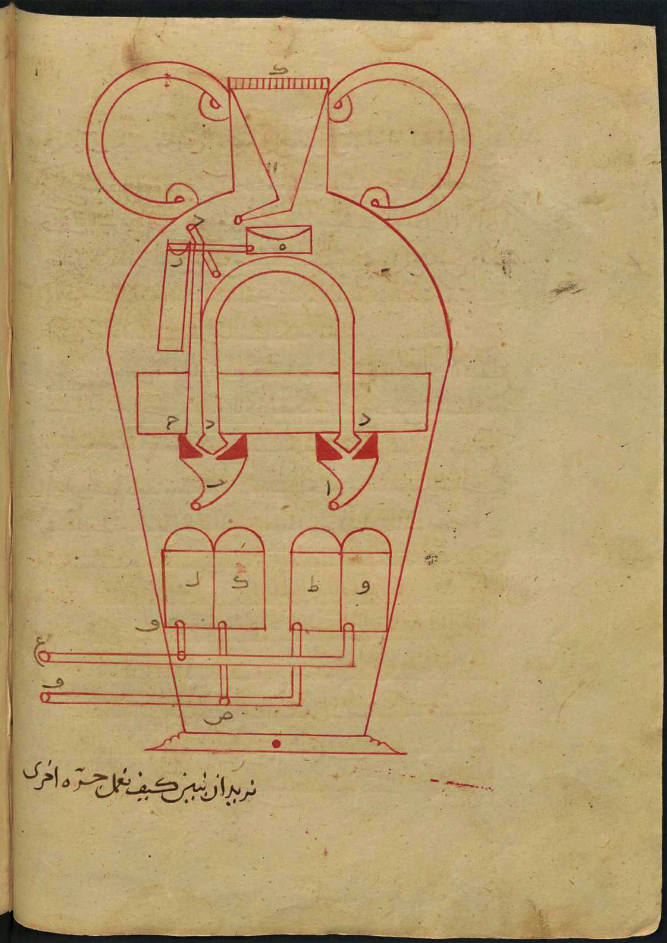
Imagen de una “jarra con trampa” del tractat sobre “aparells enginyosos” dels Banū Mūsa. Manuscrit Staatsbibliothek zu Berlin, Ms. or. qu. 739. Wikimedia.

Queda la matemática, la esencia de las disciplinas que hemos estado revisando. De la actividad astronómica nace la trigonometría tal como la entendemos hoy en día. Ptolomeo, partiendo del teorema de Menelao, conoce básicamente la función cuerda (crd (α)= 2 sin α/2). La astronomía hindú inventó la función seno y al-Khwārizmī es el primero que presenta una tabla de senos y cosenos. Poco después Ḥabaix introduce la tangente y la cotangente. La intención de estos astrónomos es, primeramente, simplificar los cálculos y las demostraciones con una matemática más eficaz. Sus continuadores, como al-Bīrūnī, ya en el siglo siguiente, harán de la trigonometría plana y esférica un objeto de estudio en sí mismo. Al-Khwārizmī, siguiendo este espíritu de pragmatismo y simplificación, inventa el álgebra en el Kitāb al-Jabr wa-l-muqābala (Libro de la reducción o compleción y el equilibrio), dedicado a al-Maʾmūn. Su intención es poder arreglar con más eficacia problemas de orden matemático que se presentan en la vida cotidiana, como transacciones comerciales, mediciones de terrenos o particiones de herencias. A partir de seis ecuaciones modelo, al-Khwārizmī enseña, sin usar ningún tipo de simbolismo matemático porque este se desarrollará más adelante, cómo resolver ecuaciones de primer y segundo grado, y hace, además, demostraciones geométricas. Aunque se habla de precedentes en Diofante, la genialidad demostrada convirtiendo lo complejo en, relativamente, fácil, hacen que muchos consideren a al-Khwārizmī como único padre del álgebra. La otra idea también genial del autor es fijarse en la numeración decimal que empleaban los hindúes y escribir un tratado sobre ella, también dedicado al califa, del que solo se conserva la versión latina, Algoritmi de numero Indorum. De este título vienen, como es sabido, algoritmo y todas las palabras afines en diversas lenguas europeas. Junto con esta matemática innovadora nacida de la solución de problemas y la hibridación, crece la matemática griega nacida de las traducciones. El círculo de los Banū Mūsā y Thābit ibn Qurra es especialmente activa en la traducción, revisión de las traducciones y comentario de las obras de referencia: los Elementos y los Data de Euclides, la Aritmética de Nicómaco de Gerasa, las Cónicas de Apolonio de Perga y De la esfera y el cilindro de Arquímedes. Un ejemplo de cómo hacían esta labor es la intervención de los Banū Mūsā en las Cónicas de Apolonio, en las que los traductores añaden nuevos teoremas y demostraciones que las generaciones futuras de matemáticos criticarán. Los traductores/traidores se sienten cómodos ante el texto y juegan con él con la voluntad de ir más allá, y Thābit, estudiando la cuadratura de la parábola, entra en el terreno casi desconocido del cálculo infinitesimal. La fuerza que mueve a estos autores no es la solución de problemas, que también, sino otra más intensa: la sed de nuevos conocimientos. Las matemáticas son estos instrumentos que, según Platón, nos permiten empezar a conocer las verdades más altas. No en vano Thābit enseñaba a los cortesanos de Bagdad la República de Platón.

Páginas de un manuscrito del tratado de álgebra de al-Khwārizmī con demostraciones geométricas. Manuscrito Oxford, Bodleian Library MS. Huntington 214.

Este hecho, junto con el perfil intelectual extremadamente polifacético de Thābit, nos muestra otro fenómeno de la época: la concepción totalizadora del conocimiento científico, en la que las disciplinas concretas no son parcelas aisladas sino partes de un conjunto vertebrado por el conocimiento filosófico, que el sabio debe poseer en su conjunto para alcanzar la perfección intelectual, es decir, la perfección humana. Esta tendencia se intensifica a partir de la época de al-Maʾmūn, cuando florecen Thābit y otros de similar ambición como al-Kindī, Ḥunayn ibn Isḥāq o Qūsṭā ibn Lūqā.

Miquel Forcada
Universitat de Barcelona

*Traducción: Judit Gil-Farrero

Cómo citar este artículo:
Forcada, Miquel. Las ciencias en Bagdad. Sabers en acció, 2025-11-19. https://sabersenaccio.iec.cat/es/las-ciencias-en-bagdad/.

Para saber más

Puedes ampliar la información con la bibliografía y recursos disponibles.