Claudi Ptolemeu

—La summa de l’astronomia antiga i de les ciències afins.—

Malgrat l’enorme importància de Claudi Ptolemeu en la història de la ciència a l’àmbit grec tardoantic, a l’islam medieval i a l’Europa de la baixa edat mitjana i renaixentista, les dades biogràfiques que en posseïm són ben minses. Tot el que en sabem de concret, extret de la seva obra, és que realitzà observacions astronòmiques a Alexandria entre el 125 i el 141 dC (les quals utilitzà a la seva gran obra, l’Almagest). També dedicà una inscripció astronòmica en un santuari de Serapis a Cànopus, no gaire lluny d’Alexandria, de la qual només conservem còpies del text als manuscrits medievals. Podem deduir, doncs, que el seu lloc de residència principal era Alexandria, a l’Egipte greco-romà del segon segle de la nostra era.

Claudius Ptolemaeus Alexandrinus, de Pedro Berruguete o Joos van Gent (Musée du Louvre). Wikimedia.

El nom “Ptolemeu” era molt popular a la província d’Egipte, per haver estat el nom dels governants masculins de la dinastia macedònica que s’hi instal·là a l’època hel·lenística. Sens dubte, aquest nom i la manca d’altres informacions biogràfiques promogueren la suposició errònia que Claudi Ptolemeu fou un rei egipci, la qual veiem reflectida a la corona i a la roba règia del retrat que originalment decorava l’studiolo de Federico da Montefeltro al palau ducal d’Urbino; dins del grup de 28 retrats de personalitats antigues i modernes relacionades amb el món del coneixement, Ptolemeu figurava al costat dels filòsofs Plató, Aristòtil i Boeci.

L’equívoc amb els monarques hel·lenístics ja el trobem a fonts àrabs anteriors com Abu Ma‘shar (s. IX), que a la seva Gran introducció als judicis de les estrelles (IV 1) diu que Ptolemeu “el savi”, el qual composà l’Almagest, fou un dels reis Ptolemeus que governaren Egipte després d’Alexandre el Gran. Curiosament, tot seguit d’aquesta afirmació, Abu Ma‘shar posa en dubte que fos el mateix autor que escriví l’obra astrològica anomenada Tetrabiblos; dubte que ressorgí entre els estudiosos alemanys del segle XIX, que no creien que un autor d’una astronomia matemàtica complexa com la de l’Almagest hagués escrit un llibre d’astrologia. Tornant al retrat de l’studiolo d’Urbino, que pot ser de Pedro Berruguete o de Joos van Gent, el turbant seria una mera indicació que el nostre savi era del nord d’Àfrica, però l’instrument que porta a la mà sí que té una tradició ben autèntica, ja que Ptolemeu mateix en descriu la construcció a l’Almagest (V 1): es tracta d’un astrolabi esfèric o esfera armil·lar, que servia tant per visualitzar la complexa geometria esfèrica dels moviments celestes (la terra hi era representada com la bola central) com per fer de manera senzilla i aproximada càlculs astronòmics complexos que requerien l’ús de taules.

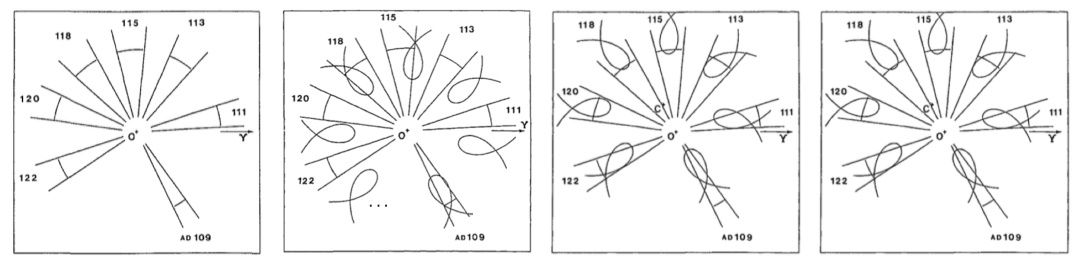
Arcs de retrogradació de Mart entre els anys 109 i 122 dC (1), superposats als tirabuixons descrits per un epicicle (2), per un epicicle amb òrbita excèntrica (3) i per un epicicle amb òrbita excèntrica i equant (4). Evans, James. The history and practice of ancient astronomy. Oxford: OUP; 1998.

Claudi Ptolemeu és, per dir-ho així, l’astrònom antic: la seva teoria planetària aconseguia finalment modelar geomètricament i de manera precisa els moviments dels cossos astrals. Això era gràcies a la invenció de l’equant —probablement atribuïble a ell mateix, tot i que l’autor prefereix mantenir un perfil baix (però alhora universalitzant) aquí com gairebé a tot arreu de la seva obra—; l’equant representava un tercer element concebut com a centre desplaçat de velocitat angular uniforme que, sumat a l’epicicle i a l’òrbita excèntrica, contribuïa a descriure la longitud al llarg de l’eclíptica (l’eclíptica és el camí del sol al llarg de l’any des de la perspectiva geocèntrica) de les òrbites planetàries en tota la seva irregularitat.

Hiparc (s. II aC) ja havia bastit una teoria geomètrica per als moviments del sol i de la lluna —de la qual només en podem llegir referències dins de l’Almagest i dels comentaris antics a l’Almagest, de Teó i Pappus—, però no per als planetes. Els astrònoms i astròlegs grecs conegueren els mètodes iteratius aritmètics usats des del segle V aC pels babilonis (en tenim testimoniat el seu ús en papirs grecs d’època imperial romana), però Hiparc i Ptolemeu anaven per un altre camí, malgrat que se serviren de la tradició astronòmica babilònica per a les observacions i per a alguns paràmetres.

Ptolemeu pogué usar desenvolupaments de la geometria esfèrica grega com el teorema de Menelau (segle I dC), cosa que no hauria estat possible a l’època clàssica, en la qual la geometria de sòlids es trobava en un estat poc desenvolupat, tal i com es lamenta Plató al llibre VII de la República. En tot cas, Ptolemeu degué viure la seva gesta a la manera de l’heurēka arquimedià, ja que gravà la seva teoria astronòmica en la forma d’una llista de paràmetres a la citada inscripció de Cànopus en agraïment al déu. Per cert, tenim un altre exemple d’aquesta pràctica tan curiosa, la inscripció astronòmica trobada a Keskintos, Rodes, que fou dedicada a “tots els déus i les dees” per un astrònom anònim probablement al segle I aC.

Ptolemeu escriví l’obra total de l’astronomia antiga, l’Almagest. Aquest caràcter ja es reflecteix al seu títol original (Composició astronòmica), però encara més en l’arabització del grec megistē, ‘la més gran (sc. composició)’, que ha acabat donant el seu nom més popular. És per això que l’obra de Ptolemeu es copià i es conservà, però no la d’Hiparc, d’un caràcter més parcial. Però és que, a banda de l’Almagest, Ptolemeu escriví unes quantes obres astronòmiques més, totes dedicades a un desconegut Sirus, el nom del qual significava ‘sirià’, cosa que probablement indica un origen en aquella regió i una nissaga servil. No sabem si era un patró ric o un jove interessat en l’astronomia, però probablement Ptolemeu no el veia com un col·lega al seu nivell, ja que altrament ens podríem esperar que ho hauria fet constar. En tot cas, ell i un tal Teó, de qui pren una sèrie d’observacions astronòmiques (Almagest IX 9, X 1-2) són els únics contemporanis que esmenta a tota la seva obra. La sensació general és de soledat: a diferència del món islàmic medieval, on tenim testimoniats nombrosos contactes i col·laboracions entre matemàtics, el món astronòmic grec és més aviat petit, fins i tot si comptem amb el factor de la menor conservació de les fonts.

Primera pàgina del calendari de Fases de les estrelles fixes en l’edició de Heiberg: “Thoth (~setembre)/ 1r (dia): 14 1/2 hores (=latitud corresponent a 14 1/2 hores solars al solstici=latitud de Rodes): l’estrella de la cua de Leo surt (=surt alhora que el sol per l’horitzó); segons Hiparc, els vents estivals s’aturen; segons Eudox, pluja, tempestes, i els vents estivals s’aturen./ 2n (dia): 14 hores (=latitud corresponent a 14 hores solars al solstici=latitud del Baix Egipte): l’estrella de la cua de Leo surt, i Spica es pon; segons Hiparc, canvi de temps. 3r (dia) (…)”. Heiberg, J. L., Claudii Ptolemaei Opera astronomica minora. Lepzig: Teubner; 1907.

De la resta d’obres astronòmiques, un parell són derivades de l’Almagest: les Hipòtesis planetàries, on descriu un model físic que podria servir de base per a un planetari, on encabia la teoria astronòmica de l’Almagest, i les Taules manejables, formada per un conjunt de taules astronòmiques derivades de les d’aquesta mateixa obra, i formatades de manera convenient per als astròlegs (però no de manera declarada). Les altres tres tracten qüestions de projecció de l’esfera en el pla —l’Analemma en relació al moviment solar observat en les ombres sobre la Terra i el Planisferi per al mapa de les estrelles fixes— i les eixides i postes de les estrelles fixes (Fases de les estrelles fixes).

Sense arribar a cobrir tants camps del saber com un al-Kindi o un Avicenna, Ptolemeu ja adopta en certa manera la figura que segles més tard veurem en els savis islàmics. En efecte, a més d’astronomia (sens dubte el seu camp predilecte), Ptolemeu cultivà l’astrologia, la geografia, la teoria musical i l’epistemologia. El seu text astrològic —Tetrabiblos, ‘Quatre llibres’, originalment intitulat Apotelesmatika, ‘Efectes astrològics’— no és ni de bon tros una obra menyspreable, sinó que representa un esforç enorme de síntesi i alhora d’explicació el més racional possible de les doctrines astrològiques més corrents de l’època, precedida per una introducció on desenvolupa una defensa de la possibilitat i la utilitat de l’art astrològica.

L’astrologia grosso modo com la coneixem avui en dia havia estat creada al món greco-romà del segle II aC (concretament a Egipte) a partir d’elements majoritàriament babilònics, i a l’època de Ptolemeu gaudia d’un cert èxit en totes les capes de la societat; però també era posada en dubte, com testimonia Ciceró a Sobre l’endevinació. A diferència de la pràctica d’endevinació astral al món babilònic, desenvolupada internament i per part d’escribes associats als temples principals, al món greco-romà l’astrologia havia estat implantada al costat de disciplines que s’entenien fins a cert punt com a racionals i auto-justificades, com la medicina o la matemàtica. És per això que els primers tractats astrològics grecs eren en forma poètica i suposadament inspirats per la divinitat; poc a poc van anar sorgint tractats en prosa, el més científic dels quals fou el de Ptolemeu.

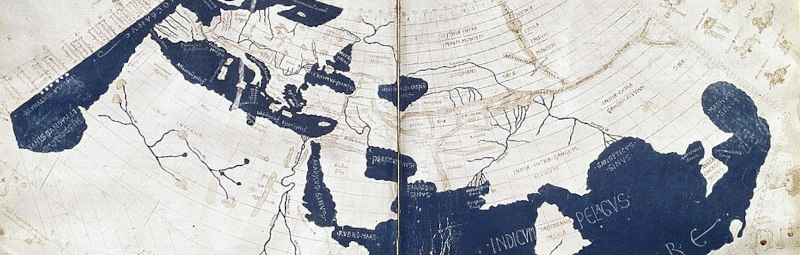
Mapa no conservat en l’original grec de la oikoumenē gē (‘terra habitada’) en la primera projecció proposada a la Guia de geografia, il·lustrat per Francesco di Antonio del Chierico a partir de la traducció llatina de Jacopo d’Angelo. Harleian MS 7182, ff. 58-59 (ca. 1465-1470). Wikimedia.

El tractat de geografia (Guia de geografia) de Ptolemeu ja s’apunta com a projecte futur a l’Almagest (II 13). Es tracta d’una obra voluminosa, en vuit llibres, sis dels quals consisteixen en una llarga taula (o més aviat una llista) amb les coordenades de les principals ciutats i accidents geogràfics (uns 8.000 punts) dins del rectangle de terra coneguda al món greco-romà del moment (la oikoumenē gē, ‘terra habitada’), computades en longitud est des de les Illes dels Benaurats (identificades amb les Canàries), i en latitud nord i sud partint de l’equador.

Les mesures geogràfiques s’obtenien tant d’observacions astronòmiques com d’estimacions basades en informacions de viatgers. Les mesures en longitud eren el major problema, i no resulta sorprenent que justament el major error de l’obra sigui una sobreestimació general en aquesta coordenada. La Guia de geografia representa el segon atles geogràfico-matemàtic del qual tenim constància: es pensa que originalment contenia mapes, els quals van desaparèixer i es van reconstruir al Renaixement. Com de costum, coneixem la tradició anterior gràcies a l’obra mateixa de Ptolemeu, ja que comença amb una crítica a l’atles de Marinos de Tir (entre els segles I i II dC) per adequar-se només a una geografia limitada en l’espai i per representar meridians i paral·lels amb línies rectes paral·leles. Ptolemeu proposa projeccions més adequades de l’esfera sobre el pla.

L’instrument de l’Orient Mitjà anomenat qānūn rep la seva denominació de l’instrument del teòric musical grec antic (kanōn). Wikimedia.

Una altra obra de Ptolemeu és l’Harmònica (literalment, ‘Coses en relació amb l’harmonia’), la qual és de gran interès per a la història de la música i de teoria musical. Aquest text pren el relleu de projectes anteriors —des de l’antic pitagòric Àrquitas (segles V-IV aC) fins el més proper en el temps del músic Dídim (segle I dC)— de descriure matemàticament, en termes de proporcions numèriques, les escales musicals usades a la pràctica musical. Igual que Dídim, Ptolemeu utilitza un instrument propi dels teòrics de la música grega, inventat en època hel·lenística, el kanōn, consistent en una o múltiples cordes tensades sobre una superfície plana i reglada, amb uns ponts mòbils que permetien mesurar la llargada de les cordes. L’instrument de l’Orient Mitjà anomenat qānūn és deutor d’aquesta denominació grega, si bé probablement tenen tradicions independents. El kanōn s’utilitza per comprovar amb l’audició les distàncies intervàliques proposades pel teòric musical: Ptolemeu mateix n’explica la construcció, de manera que el lector en principi podia fer totes les comprovacions que s’indiquen al tractat. El punt culminant del text són una sèrie de taules que descriuen amb tota precisió la posició dels ponts que reproduïen totes les notes de les escales tradicionals gregues, en tots els modes possibles. El tractat també és interessantíssim per la seva discussió epistemològica, la qual incorpora definicions musicals del peripatètic Aristoxen, i també per la secció final, consistent en un excurs que posa en relació els elements pitagòrico-platònics de la música amb la teoria desenvolupada en el mateix tractat.

Finalment, cal destacar el breu assaig anomenat Sobre el criteri i la part regent, de contingut únicament epistemològic, sense cap referència concreta a temes matemàtics, però de clara aplicació com a fonament teòric dels seus altres tractats. De fet, en el text de l’Harmònica apareixen en una forma més succinta alguns dels temes d’aquest assaig. Ptolemeu hi presenta el concepte originalment estoic de ‘criteri’ (kritērion), que posteriorment (ja a la seva època) fou compartit per altres escoles filosòfiques i per científics interessats a desenvolupar una teoria del coneixement, com el metge Galè.

En origen, es tractava, per als estoics, de proposar l’existència d’una eina epistemològica per establir la veritat d’una hipòtesi enfront de la resta, per tal d’arribar a un coneixement vàlid. Hem de situar aquesta discussió en el context de la pugna entre estoics i acadèmics (platònics) per la qüestió de la possibilitat del coneixement, en la qual els darrers proposaven la epokhē o abstenció de judici, la qual feia impracticable, o almenys difícil, la noció de ciència. L’aplicació del criteri a ciències com l’astronomia és proposada per primer cop explícitament per l’estoic Posidoni (inici segle I aC), i d’alguna manera implica una continuïtat entre la filosofia natural, tradicionalment practicada des d’una certa distància per part del filòsof, i les ciències matemàtiques. Posidoni mateix és filòsof i alhora científic.

Que Ptolemeu és hereu d’aquesta tradició, i que té un interès evident a presentar-se com un filòsof (a més d’astrònom i matemàtic), es fa evident ja a l’intel·ligent i intricat prefaci de l’Almagest, en el qual defineix i classifica l’astronomia i la matemàtica com a disciplines internes a la filosofia, utilitzant declaradament (però d’una manera lleument esbiaixada) una vella classificació de la Metafísica d’Aristòtil (1026a). La referència a l’antic mestre tampoc no és casual, ja que d’alguna manera el projecte ptolemaic de tractar tots els camps de la matemàtica aplicada té un paral·lel amb l’enciclopedisme peripatètic. En efecte, ningú abans que Ptolemeu no havia estudiat en profunditat i de manera interconnectada disciplines de la matemàtica aplicada com l’astronomia, l’astrologia, la geografia i la teoria musical.

Cristian Tolsa
Universitat de Barcelona

Com citar aquest article:
Tolsa, Cristian. Claudi Ptolemeu. Sabers en acció, 05-02-2025. https://sabersenaccio.iec.cat/claudi-ptolemeu/.

Per a saber-ne més

Pots ampliar la informació amb la bibliografia i recursos disponibles.