Les ciències a Bagdad

—L’astronomia, l’astrologia i les disciplines matemàtiques durant el segle IX.—

La disciplina més important durant el califat d’al-Manṣūr fou l’astrologia, que era considerada com una ciència d’acord amb l’epistemologia aristotèlica. Al-Kindī (m. 876), el gran filòsof de l’època, i el seu deixeble Abū Maʿxar (787-886), un dels astròlegs més importants, ho sostingueren amb fermesa i bons arguments. Els astròlegs d’al-Manṣūr eren majoritàriament d’origen persa (Nawbakht i la seva nombrosa descendència, Māixāʾallāh, ʿUmar ibn Farrukhān al-Ṭabarī), encara que n’hi havia d’altres d’origen àrab com al-Fazārī o Yaʿqūb ibn Ṭāriq. L’astrologia que practicaven devia ser essencialment la persa, que emprava els textos d’autors grecs com Doreoteu de Sidó traduïts al pehlevi, alguns del quals foren retraduïts a l’àrab per aquests astròlegs. Aquests autors eren (també i sobretot si volien ser bons astròlegs) uns astrònoms més que competents que es proveïren dels millors mitjans possible, començant per les taules astronòmiques. Algunes ja les tenien en el seu bagatge persa (Zīj al-Arkand i Zij al-Xāh), i l’any 771 o 773 arribà a Bagdad una ambaixada de l’Índia en què hi havia un astrònom que duia el Brahmasphutasidhānta, les taules astronòmiques compilades per l’hindú Brahmagupta en 629. Amb l’ajut d’aquell astrònom, al-Fazārī i Yaʿqūb ibn Ṭāriq van traduir aquestes taules que en endavant serien conegudes com a Sindhind i arribaren fins a al-Andalus. No es quedaren aquí i al-Fazārī passa per ser el primer constructor musulmà d’un astrolabi, inaugurant així una fèrtil tradició que tenia pocs precedents al món grec i siríac i que possiblement els autors de Bagdad conegueren a través de fonts siríaques. Per la seva banda, Māixāʾallāh escriví un tractat cosmològic en què citava Ptolemeu i Aristòtil, probablement coneguts també a través de traduccions siríaques.

Pàgina del tractat astrològic sobre nativitats d’Abū Maʿxar. Es troba en un manuscrit egipci del s. XV (BNF Arabe 2583). Wikimedia.

Al-Maʾmūn donà un fort impuls a l’astronomia envoltant-se d’una nova generació d’astrònoms/astròlegs entre els que hi havia persones molt brillants com al-Kwārizmī, Ḥabaix al-Ḥāsib, els germans Banū Mūsā o Yaḥyā b. Abī Manṣūr o el menys conegut, en termes biogràfics, al-Farghānī. Obsessionat per la precisió, al-Maʾmūn ordenà que es fessin observacions del cel per verificar els paràmetres de Ptolemeu (llavors ja s’havien fet dues traduccions de l’Almagest, es traduí una tercera vegada per a al-Maʾmūn i encara se’n farien dues versions més en el segle IX). Les primeres observacions es feren entre 828 i 829 a un barri de Bagdad anomenat Xammasiyya i com que no es quedaren del tot satisfets, se’n feren de noves a Damasc entre 831 i 832.

En aquests indrets s’hi construïren sengles observatoris, els primers en la història de l’islam, que probablement s’equiparen amb instruments d’observació similars als descrits per Ptolemeu a l’Almagest. De les observacions fetes se’n derivaren diverses taules astronòmiques començant per l’oficial, que s’anomenà al-Zīj al-mumtaḥan, “les taules comprovades”, compilades per Yaḥyā b. Abī Manṣūr. Entre els paràmetres que es corregiren a Ptolemeu per ajustar-los més a la realitat n’hi alguns de tan importants com l’obliqüitat de l’eclíptica (23;51° segons Ptolemeu, 23;33° segons Yaḥyā b. Abī Manṣūr) o la precessió dels equinoccis (1° per segle segons Ptolemeu, 1° en 66 anys seguint models indoperses). Alguns d’aquests astrònoms com al-Khwārizmī o Ḥabaix feren les seves pròpies taules, el primer revisant les del Sindhind i el segon revisant les taules indoperses a la seva joventut i les Mumtaḥan al final de la seva vida.

Aquests astrònoms excel·liren igualment en el terreny de la instrumentació. Al-Khwārizmī és l’autor del primer tractat de construcció i ús de l’astrolabi i a Ḥabaix se li atribueix la invenció de l’astrolabi esfèric i, a més, escriví un tractat sobre un astrolabi curiós amb forma de meló. Aquests astrònoms també es preocuparen pels models cosmològics i ja Muḥammad ibn Mūsā escriví diversos tractats qüestionant els models planetaris de Ptolemeu, i, específicament, criticant que aquest postulés l’existència d’una novena esfera per explicar el moviment diürn dels astres. Aquesta línia de treball continuà fins a final de segle i prosperà notablement en el futur, donant lloc a una fèrtil tradició d’estudis i models de cosmologia matemàtica que arribaria a conèixer el mateix Copèrnic. Si bé molta de l’astronomia que es practicà tenia com a finalitat la confecció dels horòscops més perfectes possibles, cal tenir present que hi havia un interès sincer per fer bona ciència i perquè aquesta ciència fos útil. En aquest sentit, els astrònoms d’aquesta època s’esforçaren per posar l’astronomia al servei del culte islàmic. Tres aspectes foren d’especial importància: la determinació de l’aparició del creixent lunar, perquè aquest marcava l’inici del mes en el calendari islàmic i calia saber quan començava el mes de Ramadan si els núvols ocultaven la lluna; la determinació de les hores de pregària, especialment les de migdia i primera de la tarda perquè depenen de l’ombra projectada per un gnòmon; i la determinació de la direcció de la Meca (qibla, alquibla) per poder orientar bé les mesquites, per a la qual cosa els astrònoms crearen procediments geomètrics i trigonomètrics de gran exactitud.

Juntament amb aquesta ciència tan sofisticada, els filòlegs i literats compilaren, amb la intenció de preservar el lèxic i la paremiologia popular dels àrabs, els seus coneixements que podem relacionar amb la ciència. En aquest cas, es tracta de l’astronomia popular àrab, relacionada amb l’ús de les estrelles que feien els beduïns per orientar-se, i al seu coneixement empíric de les estrelles, el sol i la lluna, com a marcadors temporals, que, a més, estaven vinculats a l’aparició de fenòmens meteorològics recurrents. Les tan escasses com desitjades pluges eren l’element essencial d’aquest coneixement que avui podem anomenar etnociència i que llavors es compilà particularment en tractats sobre anwāʾ (períodes marcats per asterismes associats a pluges i altres meteors). Curiosament, potser una bona part d’aquest saber empíric naixia d’una creença astrolàtrica (de l’estil “les estrelles que apareixen regularment a la tardor causen les pluges de la tardor”) que l’islam abolí. Malgrat aquest problema, l’etnoastronomia quedà vinculada a la nova tradició cultural dels musulmans perquè els homes de religió esmenaren qualsevol problema legal amb gran finor jurídica i la gent comú aprecià el valor del llegat tradicional i la seva utilitat per a, per exemple, determinar de forma molt aproximada l’alquibla. A pesar el seu caràcter no científic, es curiós constatar com els autors d’aquests tractats manllevaren conceptes de l’astronomia indopersa dels astrònoms científics (segons els estàndards de l’època).

Però aquesta mena de coneixement és perifèric en el saber de l’època, en què la precisió de la ciència impera. En el Llibre dels cossos i les distàncies de Ḥabaix al-Ḥāsib, es diu que el califa al-Maʾmūn volia saber la qibla de la Meca des de Bagdad i ordenà que es calculés la diferència de longituds entre la Meca i Bagdad mitjançant l’observació d’un eclipsi lunar a totes dues ciutats. El mètode ja l’havien usat Hiparc i Ptolemeu. L’eclipsi té lloc al mateix moment però en una hora diferent a cada ciutat. Si sabem la diferència de l’hora entre les dues ciutats, considerant que una hora equival a 15^o de l’esfera, podem trobar aproximadament la diferència de longitud, que al text s’estima en uns 3^o. La diferència de latitud era fàcil de calcular amb només la posició del sol. Les dades obtingudes permeten, mitjançant procediments geomètrics i trigonomètrics, no sols obtenir la direcció de la Meca sinó la distància entre Bagdad i la Meca tenint en compte quantes milles corresponen a un grau de l’esfera. En el text, un grau correspon a 56 milles, i la línia més directa entre les dues ciutats (la que traçaria “una fletxa que volés per l’aire”), s’estima en 676 milles i 2/3, mentre que es constata que la distància real del camí és de 712. El califa dona per bona la diferència atès que en el camí hi ha moltes pujades i baixades. Aquesta reveladora anècdota s’inclou en un llibre que tracta, essencialment, d’una altra de les obsessions d’al-Maʾmūn, la determinació de la distància exacta de la Terra per posar al dia el famós amidament d’Eratòstenes. Ḥabaix ens parla d’una expedició ordenada pel califa a aquest efecte, amb un equip d’astrònoms ben proveït, i d’altres fonts ens parlen d’una altra en què l’equip científic estaria format pels germans Banū Mūsā i, potser, al-Khwārizmī. El problema dels relats és que no acaben de coincidir en l’equivalència entre graus i milles àrabs, però en l’aproximació més optimista (un grau, 56 milles 2/3 i una milla àrab, ca. 111,12 km), el valor de la circumferència de la Terra s’apropa molt al real de 40.007,863 km.

Pàgina d’un manuscrit del Llibre de la forma de la terra d’al-Khwārizmī, en què es representa el Nil. Manuscrit Strasbourg, Bibliothèque Nationale et Universitaire, Ms 4.247. Wikimedia.

Amb independència de les discrepàncies de les narratives, sembla evident que tal expedició existí i que forma part d’un altre dels projectes d’al-Maʾmūn: conèixer la terra tan bé com el cel, cosa que té tot el sentit si pensem que un governant ha de tenir el coneixement més precís possible del territori. El califa donà un impuls decisiu a la geometria matemàtica i la cartografia, encara que els detalls del procés encara se’ns escapen. Sembla ser que la Geografia de Ptolemeu (i potser també la de Marí de Tir) ja circulava per Bagdad a l’època d’al-Maʾmūn i aquest hauria ordenat a un equip de geògrafs, que podia ben bé coincidir amb el d’astrònoms (de fet, els principis de projecció de la cartografia són similars als de la projecció dels instruments astronòmics), la preparació d’uns mapes de la Terra. Segons un dels grans experts en el tema, Fuat Sezgin, encara quedaria un mapamundi d’aquests transmès pel geògraf i historiador al-ʿUmarī (m. 1349). Segons Sezgin, i això és controvertit però interessant, aquest mapa seria una novetat ja que Ptolemeu explica com fer mapes, però no en feu a la pràctica. El que ens queda és un Kitāb Ṣūrat al-arḍ (Llibre sobre la forma de la Terra) d’al-Khwārizmī (segons Sezgin, no caldria identificar-lo necessàriament amb el famós astrònom i matemàtic), que consisteix principalment en una llarga llista de coordinades geogràfiques de moltes localitats. Aquest tractat és coherent amb el mapa, que dibuixa un món més realista, amb un oceà Índic que no és un gran llac tancat, a diferència de les representacions gregues, i un mar Mediterrani ajustat a les seves veritables proporcions.

Altres disciplines basades en la matematització del món (com la música o l’òptica) floriren en el període gràcies a les traduccions de les fonts gregues. D’aquestes, la més important en el període és l’estàtica, la ciència “dels pesos”, que és al darrere de la tècnica de construcció de les balances i és també el principi de la mecànica desenvolupada entre els grecs per Heró d’Alexandria o Filó de Bizanci. Els més destacats foren els Banū Mūsa, autors d’un Kitāb al-Ḥiyal que el gran expert en el tema, Donald Hill, tradueix com a “Book of ingenious devices” o “Llibre dels dispositius enginyós”. En ell es descriuen més d’un centenar d’aparells destinats essencialment a la diversió i a la pedagogia. Es tracta d’autòmats com un flautista que toca una flauta que fa música gràcies a un complex instrument hidràulic; o d’artefactes que produeixen tot d’efectes sorprenents, com una gerra on s’hi aboquen líquids de tres colors diferents i quan s’obre una aixeta els líquids surten en l’ordre en què s’han posat. Es tracta d’un aprofitament lúdic de l’energia de l’aigua i l’aire mitjançant vàlvules, engranatges i pistons que, en endavant, encara se sofisticarà més i permetrà de disposar d’enginys més complexos per a un ús civil. En qualsevol cas, els Banū Mūsā i d’altres com al-Farghānī actuaren d’enginyers per als califes en infraestructures complexes, encara que de les tècniques emprades no n’han quedat referències escrites.

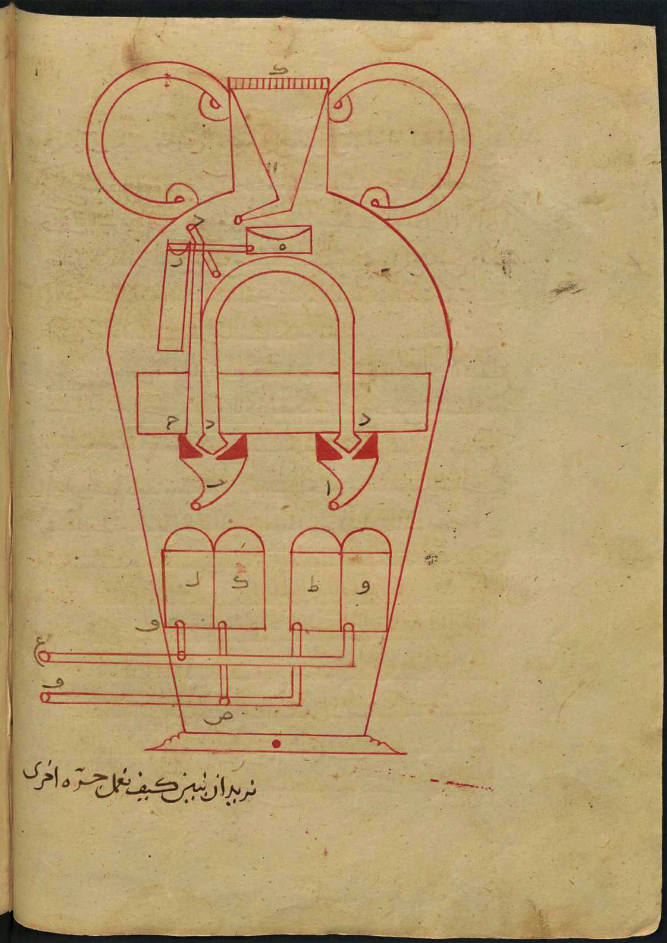
Imatge d’una “gerra amb trampa” del tractat sobre “aparells enginyosos” dels Banū Mūsa. Manuscrit Staatsbibliothek zu Berlin, Ms. or. qu. 739. Wikimedia.

Queda la matemàtica, l’essència de les disciplines que hem estat revisant. De l’activitat astronòmica neix la trigonometria tal com l’entenem avui en dia. Ptolemeu, partint del teorema de Menelao, coneix bàsicament la funció corda (crd (α)= 2 sin α/2). L’astronomia hindú inventà la funció sinus i al-Khwārizmī és el primer que presenta una taula de sinus i cosinus. Poc després Ḥabaix introdueix la tangent i la cotangent. La intenció d’aquests astrònoms és, primerament, simplificar els càlculs i les demostracions amb una matemàtica més eficaç. Els seus continuadors, com al-Bīrūnī, ja el segle següent, faran de la trigonometria plana i esfèrica un objecte d’estudi en si mateix. Al-Khwārizmī, seguint aquest esperit de pragmatisme i simplificació, inventa l’àlgebra en el Kitāb al-Jabr wa-l-muqābala (Llibre de la reducció o compleció i l’equilibri), dedicat a al-Maʾmūn. La seva intenció és poder arreglar amb més eficàcia problemes d’ordre matemàtic que es presenten a la vida quotidiana, com transaccions comercials, amidaments de terrenys o particions d’herències. A partir de sis equacions model, al-Khwārizmī ensenya, sense usar cap mena de simbolisme matemàtic perquè aquest es desenvoluparà més endavant, com resoldre equacions de primer i segon grau, i fa, a més, demostracions geomètriques. Tot i que es parla de precedents en Diofant, la genialitat demostrada convertint el complex en, relativament, fàcil, fan que molts considerin al-Khwārizmī com a únic pare de l’àlgebra. L’altra idea també genial de l’autor és fixar-se en la numeració decimal que empraven els hindús i escriure’n un tractat, també dedicat al califa, del qual només es conserva la versió llatina, Algoritmi de numero Indorum. D’aquest títol venen, com és sabut, algoritme i totes les paraules afins en diverses llengües europees. Junt amb aquesta matemàtica innovadora nascuda de la solució de problemes i la hibridació, hi creix la matemàtica grega nascuda de les traduccions. El cercle dels Banū Mūsā i Thābit ibn Qurra és especialment actiu en la traducció, revisió de les traduccions i comentari de les obres de referència: els Elements i els Data d’Euclides, l’Aritmètica de Nicòmac de Gerasa, les Còniques d’Apol·loni de Perga i De l’esfera i el cilindre d’Arquímides. Un exemple d’aquesta manera de fer és la intervenció dels Banū Mūsā a les Còniques d’Apol·loni, en què els traductors hi afegeixen nous teoremes i demostracions que les generacions futures de matemàtics criticaran. Els traductors/traïdors se senten còmodes davant del text i juguen amb ell amb la voluntat d’anar més enllà, i Thābit, estudiant la quadratura de la paràbola, entra en el terreny gairebé desconegut del càlcul infinitesimal. La força que mou aquests autors no és la solució de problemes, que també, sinó una altra de més intensa: la set de nou coneixement. Les matemàtiques són aquest instrument que, segons Plató, ens permet de començar a conèixer les veritats més altes. No en va Thābit ensenyava als cortesans de Bagdad la República de Plató.

Pàgines d’un manuscrit del tractat d’àlgebra d’al-Khwārizmī amb demostracions geomètriques. Manuscrit Oxford, Bodleian Library MS. Huntington 214.

Aquest fet, juntament amb el perfil intel·lectual extremadament polifacètic de Thābit, ens mostra un altre fenomen de l’època: la concepció totalitzadora del coneixement científic, en què les disciplines concretes no són parcel·les aïllades sinó parts d’un conjunt vertebrat pel coneixement filosòfic, que el savi ha de posseir en el seu conjunt per assolir la perfecció intel·lectual, és a dir, la perfecció humana. Aquesta tendència s’intensifica a partir de l’època d’al-Maʾmūn, quan floreixen Thābit i altres de similar ambició com al-Kindī, Ḥunayn ibn Isḥāq o Qūsṭā ibn Lūqā.

Miquel Forcada
Universitat de Barcelona

Com citar aquest article:
Forcada, Miquel. Les ciències a Bagdad. Sabers en acció, 19-11-2025. https://sabersenaccio.iec.cat/les-ciencies-a-bagdad/.

Per a saber-ne més

Pots ampliar la informació amb la bibliografia i recursos disponibles.